Poisson Distribution

poisson distribution is a discrete distribution because the random variable denotes the number of events occurences in a fixed time period.
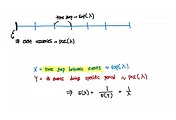
- discrete distribution
- x: number of event occurences in a fixed time period (discrete numbers)
Poisson Axioms
1. when time interval is small enough, probability that more than one event happens is 0.
2. event occurences are independent in two intervals which are not overlapped.
3. the number of events occurences is proportional to time interval.


when the random variable X follows poisson distribution with mean λ , it is denoted as X~POIS(λ )
In other words, λ is the mean of poisson distribution that is average rate of events.
Example of Poisson distribution
* the number of flights landing in an hour
* the number of typos in a page
* the number of calls in an hour
Examples that Violate Poisson Axioms ( cannot apply for poisson distribution )
*the number of earthquake during a year in Japan
In such a case, the event occurences cannot be independent because previous earthquakes tend to affect next earthquake so we cannot apply poisson distribution to this case.
PMF(Probability Mass Function) of Poisson distribution

where λ is greater than 0
and x is greater than, equal to 0 and discrete numbers (x=0,1,2,..)
because random variable X should be discrete numbers in discrete distributions and X denotes the number of events occurences so it should not be a negative number.
E(X) and Var(X) of Poisson distribution
If, X follows poisson distribution with parameter lambda,
X~POIS(λ )
E(X)=λ
Var(X)=λ
So if X follows Poisson distribution, and E(X)=3, you can say, X~POIS(3)
Application of Poisson distribution
Q:
If 4 calls are recieved every 7 hours on average, compute P("recieve 3 call ring in 5 hours")
and compute P("recieve at least 3 calls in 5 hours")
First, determine whether you can apply poisson distribution to this case or not.
Poisson Axioms
1. when time interval is small enough, probability that more than one event happens is 0.
→you can divide time intervals many times until probability that more than one event happen became close to 0 for this case.
ex) you can divide time interval many times for it to become 5 seconds for each interval, there are only two cases can happen during the interval which are one call rings or no call rings. That is, P(X>=2)=0.
2. event occurences are independent in two intervals which are not overlapped.
→call rings are independent for each other. a call does not affect the occurence of next and previous calls.
3. the number of events occurences is proportional to time interval.
→ the fact that you recieve 4 calls every 7 hours on average can imply you will recieve 8 calls every 14 hours on average.
Answer:
we can start solving this problem by finding expected value of number of calls in an hour.
"4 calls are recieved every 7 hours on average"
→X: the number of calls during the time unit(an hour)
→ E(X)=4/7
→ so, X~POIS(4/7)


Property of Poisson distribution
Smaller λ , Higher Skewness

'Statistics' 카테고리의 다른 글
| Markov's Inequality 마르코프 부등식 (0) | 2020.07.23 |
|---|---|
| Covariance & Correlation Coefficient /Property of Covariance (0) | 2020.07.15 |
| Relationship between Exponential and Poisson distribution 지수분포와 포아송 분포의 관계 (0) | 2020.07.14 |
| Memoryless Property of exponential and geometric distribution 지수분포와 기하분포의 무기억성 (0) | 2020.07.14 |
| Relationship between Exponential and Gamma distribution 지수분포 감마분포 관계 (0) | 2020.07.14 |