Variance measures the spread of random variable around its mean.
Covariance measures the direction of linear relationship between two random variables. That is, it is a measure of the scattered relation between two random variables.
Cov(X,Y) = E(X-E(X)) E(Y-E(Y))

Covariance is usually computed with E(XY)-E(X)E(Y) rather than Cov(X,Y) = E(X-E(X)) E(Y-E(Y))
According to the meaning of Covariance between X, Y is the measure of the scattered relation between X and Y ,
Covariance between X and X can be interpreted ad Variance of X.
Covariance measures the direction of linear relationship between two random variables.
In other words, if Y increases when X increases, Cov(X,Y) becoms positive number because it denotes the linear relationship between two random variable. Conversely, if Y increases when X increases, Cov(X,Y) becomes negative.
If there seems no linear relationship between two random variable, Cov(X,Y) becomes 0.

No relationship between two random variable means ‘ two random variables are independent.’
IfX and Y are independent, Cov(X,Y) =0
But, Cov(X,Y)=0 does not imply X and Y are independent.

There are some properties and proofs of properties of Covariance
<Property1>
Cov(aX+b , cY+d) = ac Cov(X,Y)

<Property2>
Cov(aX+bY, cX+dY)=acVar(X)+bdVar(Y)+ (ad+bc)Cov(X,Y)

<Property3>
Cov(aX+bY, cZ+dV)= acCov(X,Z)+adCov(X,Y)+bcCov(Y,Z)+bdCov(Y,V)

<Property4>
The way to compute variance of sum of random variables.


<Property5>
Property of covariance using Cauchy Schwarz Inequality
Cauchy-Schwarz Inequality
(E(XY))^2 <= E(X^2)E(Y^2)

<Limitation>
Covariance describes how two variables are related but it is affected by magnitude of variables. That is, If X and Y are very small, covariance cannot be large even if they have strong relationship. So Covariance is not a perfect measure of relationship between 2 random variables.
<Correlation Coefficient>
Computed deviding covariance by standard deviation of X and Y.
Substitution of Covariance which covers its limitation.

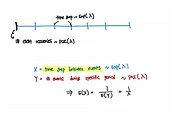
As denoted in the above image, the correlation coefficient should be between -1 and 1.
-1<= p <=1
| p=1 | perfect positive correlation |
| p=0 | no linear relationship |
| p=-1 | perfect negative correlation |

<Relation between cor(X,Y) , cor(aX+b, cY+d)>