Exponential Distribution VS Gamma Distribution
The relationship between Exponential distribution and Gamma distribution is similar to Relationship between Geometric distribution and Negative Binomial distribution.
The random variable of Gamma distribution is the sum of independent and identically distributed Exponential distribution.
As Random variable of Negative Binomial distribution is the sum of iid Geometric distribution.

Exponential Distribution
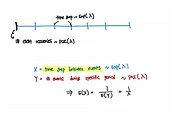
When X follows exponential distribution, X~EXP(λ)
X: the time until next event occurs.
So exponential distributon is continuous distribution because it deals with time which is continuous.
PDF(Probability Density Function) and CDF of Exponential Distribution
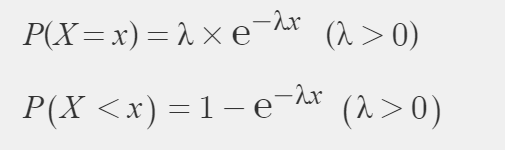
Expected value and Variance of Exponential distribution

Gamma Distribution
When X follows gamma distribution, X~GAM(R, λ)
X: Time Until Rth event occurs
Sum of R independent and identically (iid) distributed exponential random variable
PDF(Probability Density Function) of =Gamma Distribution
when X: Time until Rth event occurs
R: The number of event occurrences.
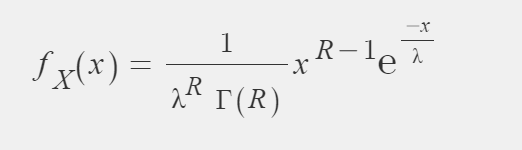
Expected value and Variance of Gamma distribution
X~GAM(R, λ )

Gamma distribution with usually used parameters
There are two notations usually used in Gamma distribution instead of using R and X

I am gonna use the second notation with parameter Alpha and Beta to prove the relationship between exponential and gamma distribution here.
Proof of relationship using pdf, E(x) and Var(x).
There are several reasons why I can say Gamma Distribution and Exponential distribution are highly related.

Firstly, I can give you the reason by substituting 1 with alpha of gamma distribution, you can see that the distribution becomes having the same distribution with exponential distribution with parameter Beta.

Also, expected value and variance of the sum of exponential distribution became expected value and variance of gamma distribution with parameter (R, lambda) where R is the total number in sum of exponential distributions and lambda is the same parameter of the exponential distribution.
Proof of relationship using moment generating function
This is direct proof using the moment generating function. Moment generating function is unique. Moment generating function of gamma distribution looks like multiplying moment generating function of exponential distribution n times.

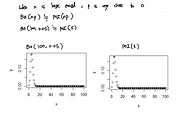
Proof of relationship Using graphs
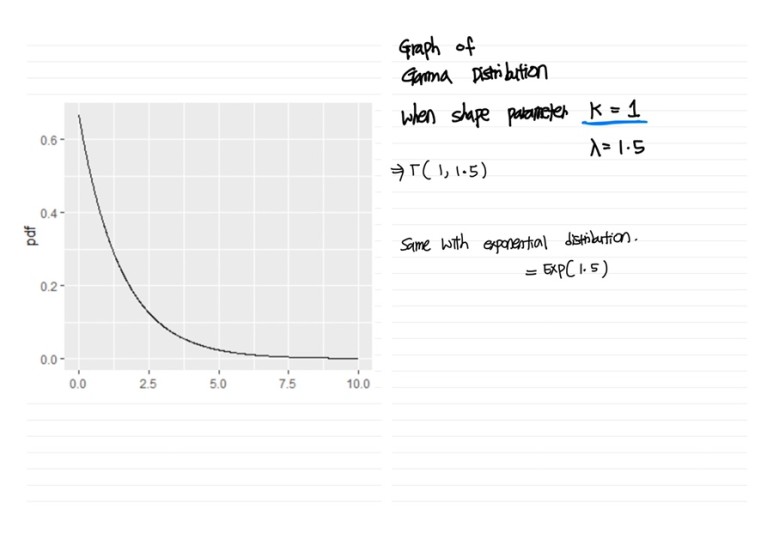
The graph of gamma distribution with shape parameter 1 is and scale parameter 1.5 looks the same with exponential distribution with parameter 1.5
In other words, gamma distribution with shape parameter 1 became exponential distribution.
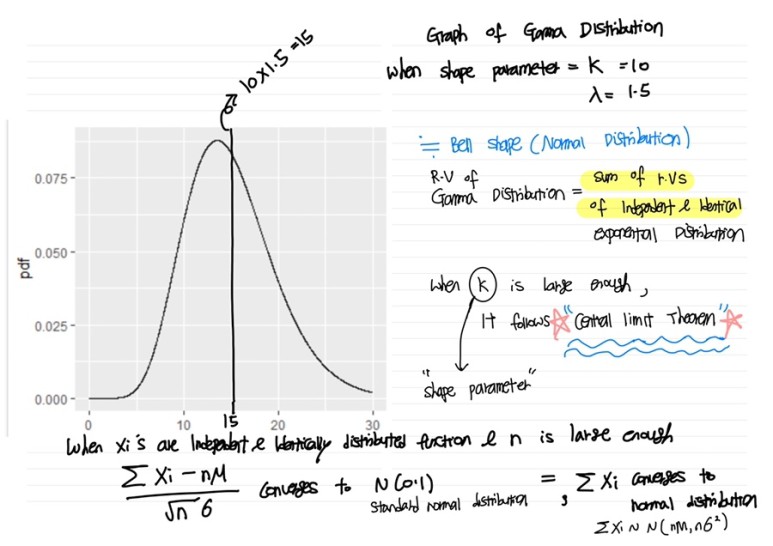
As gamma distribution is sum of independent and identically distributed exponential distribution, it follows the central limit theorem when shape parameter is large enough. So graph of gamma distribution with large shape parameter looks symmetric of its mean as it converges to normal distribution.
'Statistics' 카테고리의 다른 글
| Relationship between Exponential and Poisson distribution 지수분포와 포아송 분포의 관계 (0) | 2020.07.14 |
|---|---|
| Memoryless Property of exponential and geometric distribution 지수분포와 기하분포의 무기억성 (0) | 2020.07.14 |
| Poisson approximation to Binomial distribution 이항분포의 포아송 근사 (0) | 2020.07.14 |
| Relationship between Negative Binomial and Geometric distribution 음이항분포 기하분포 (0) | 2020.07.14 |
| Bayes Theorem 베이즈 정리 (0) | 2020.07.14 |