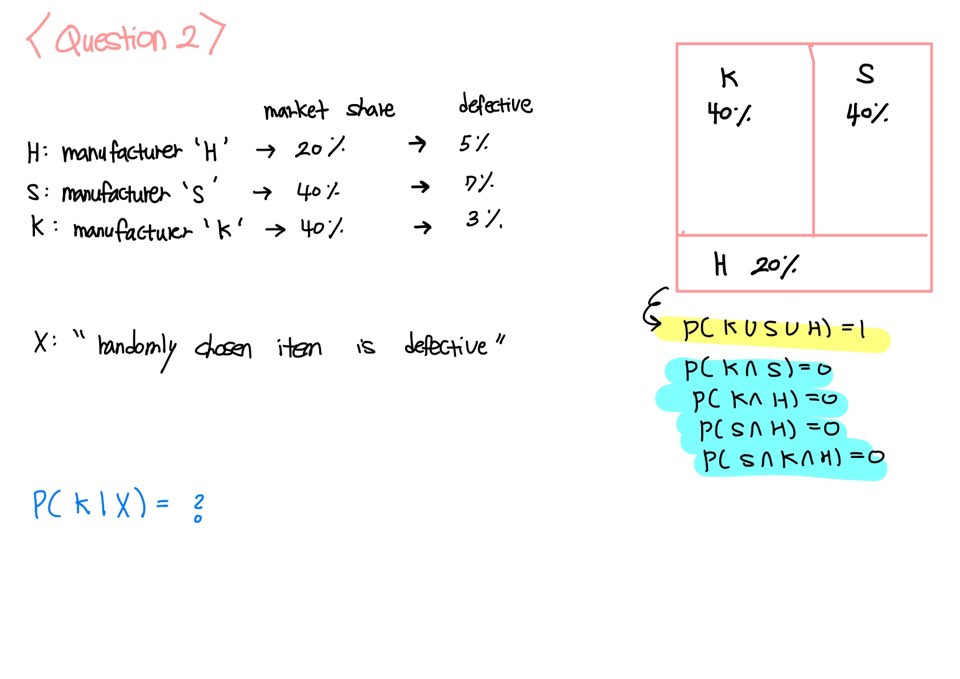
Bayes Theorem makes it possible to compute the probability of an event, which is not directly described, based on some conditions related to the event.
For example,
you can compute P(a person have cancer given the fact that the person gets + result in cancer examination)with some given probabilities ( P(+|cancer), P(+|no cancer), P(a randomly selected person get cancer )which looks not directly related with the above probability.
If it satisfies some conditions.

Bayes Theorem
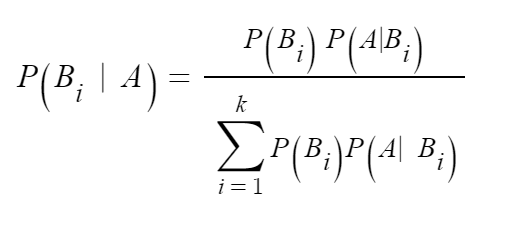
When B(i) satisfies two conditions.
Conditions For Bayes Theorem
There are two conditions to use Bayes theorem
1. events are mutually exclusive
2. events are exhaustive
If it satisfies two conditions above, you can use Bayes Theorem.
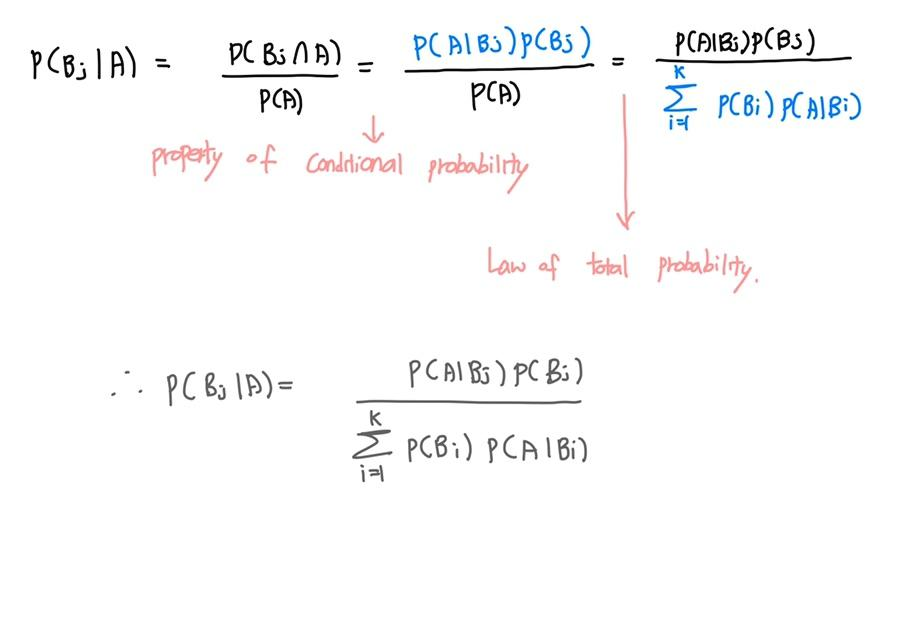
As mentioned in the image, there are two based theorems ( Law of total probability, property of conditional probability) to understand the Bayes Theorem.

Two Based Theorem in Bayes theorem
1. Property of Conditional Probability
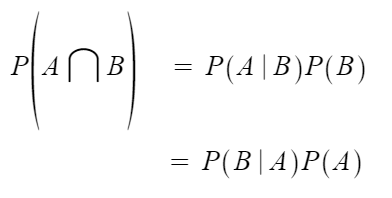
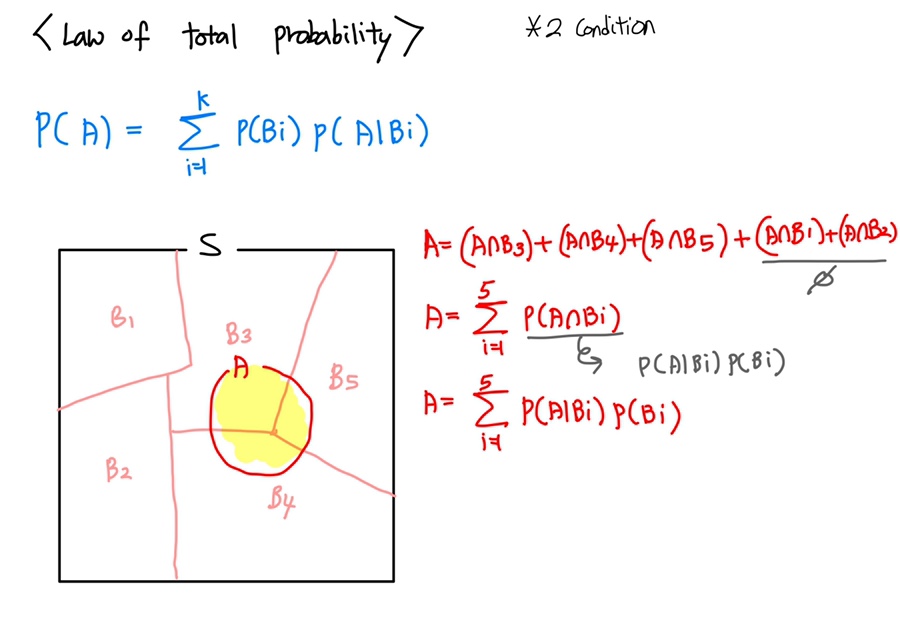
2. Law of Total Probability
Two conditions for Bayes Theorem are derived from Law of Total Probability as this theorem is used in Bayes Theorem.
So when we say Law of Total Probability, there are two conditions which are
1. events are exhaustive
2. events are mutually exclusive
Example 1
Given that
probability of getting a positive result in coronavirus examination when the person actually has coronavirus is 0.98
probability of getting a positive result in the examination when the person does not have coronavirus is 0.15
the probability that a randomly chosen person has coronavirus is 0.001
is well-known information.
with the given information, is it possible to compute
the probability that a person has coronavirus when the person has a positive result?
Using Bayes theorem, you can compute the probability with given information.

Before deciding to apply Bayes Theorem, you should check whether the event of coronavirus satisfies conditions for Bayes Theorem (exhaustive, exclusive) or not.

The Event of getting corona satisfies two conditions (exhaustive, exclusive.)
So we can use Bayes Theorem.

Example2