숫자로 표현된 설명변수와 반응변수의 관계를 파악하고, 이를 설명하는 최적의 회귀식을 찾는것을, 양적자료(quantitative data)를 기반으로 한 회귀분석 이라고 할 수 있습니다. 설명변수와 반응변수의 선형 관계를 파악하기 위해서는 주로 연속적 표현이 가능한 양적자료가 많이 사용되지만, 종종 질적 자료(qualitative data)를 설명변수로 채택해야하는 경우도 생기기 마련입니다.
양적자료와 질적자료에 대한 간략한 설명을 덧붙이자면,
양적자료란, 수치로 측정하고 표현하는것이 가능한 자료입니다. 따라서, 수치형 자료(numerical data)로도 불리우죠.
질적자료(qualitative data)란, 수치로 측정 및 표시가 불가능한 자료입니다. 성별 혹은 혈액형과 같이 집단을 구분하는 변수로서, 수치로 표현이 불가능한 분류 대상을 질적자료라고 하죠. 이는 범주형 자료(categorical data)로도 불립니다.
범주형 자료가 설명변수로서, 회귀모형에 포함되는 경우를 살펴봅시다.
앞선 블로그에서, 개념적 내용을 다뤘으니, 이해가 안되는 내용이 있다면, 참고해주세요:)
[회귀]지수변수를 설명변수로서 포함한 회귀 모형, 교호작용에 대한 설명/ Indicator variable in regress
숫자로 표현된 설명변수와 반응변수의 관계를 파악하고, 이를 설명하는 최적의 회귀식을 찾는것을, 양적자료(quantitative data)를 기반으로 한 회귀분석 이라고 할 수 있습니다. 양적자료란, 수치로
jangpiano-science.tistory.com
범주형 자료의 예시로 가장 자주 언급되는것은 '성별(gender)' 입니다. Man/Female 이라는 이분법적 범주 역시 회귀모형에서 설명변수를 예측하는데 중요한 영향을 미칠 수 있습니다. 예를들어, 반응변수를 성인이 하루에 섭취하는 칼로리의 양이라고 할때, 키, 몸무게 이외에도 샘플의 성별 역시 반응변수에 큰 영향을 미칠 수 있겠죠?
<지시변수 indicator variable>
범주형 자료의 구체적인 예를 생각해보았을때, 성별 혹은 질병의 유무를 들 수 있습니다.
지시변수는, 범주형 자료를 숫자로 표현한 변수라고 할 수 있습니다. 지시변수는, 0과 1 만으로 표현되며, 각각 범주의 영향이 있느냐, 없느냐를 의미합니다. 범주의 영향이 있는 경우, I = 1 로 표현, 범주의 영향이 없는 경우, I = 0으로 표현합니다.
0과 1로 표현되는 지시변수는, 상호배타적(Mutually exclusive) 이라는 특징을 가지고 있습니다. 0과 1이라는 변수 사이에 교집합이 존재하지 않음을 의미하죠.
지시변수가 포함된 회귀식에 대해서, 지시변수의 필요성에 대해서는, 지시변수 앞의 회귀계수가 유의한지에 대한 검정을 통해 알 수 있습니다. 회귀식을 Y = B0 + B1*X + B2*I + ε 라고 하였을때 , I의 유의성에 대한 검정은 다음과 같습니다.
H0 : B2 = 0
따라서, H0이 기각되는 경우, I라는 지시변수가 표현하는 범주형 자료가 Y에 영향을 미친다고 결론 내릴 수 있습니다.
지시변수가 회귀모형이 포함되는 경우를 살펴봅시다.
<두개의 범주(levels)를 포함한 범주형 변수>
선형 회귀 모형에서 범주형 변수를 설명변수로 포함하기 위해서는, 우선 해당 변수의 데이터 타입을 확인해야 합니다.
회귀 분석은, 변수로서 수치형 자료(numerical variable)를 필요로 하기 때문이죠.
위에서의 예시를 인용해 설명해보겠습니다.
샘플에서 성별 데이터가 Male, Female 과 같이 문자형 요인(character factor) 표현된 경우에 0, 1 과같은 수치형 변수로 바꿔주어야, 회귀모형에 포함 할 수가 있습니다.
모형의 설명변수에 문자형 요인으로 표현되는 범주형 변수가 포함되는 경우, R 에서는 해당 변수를 지시변수로 자동변환해 회귀적합을 진행합니다.
contrasts(Salaries$sex)
# Male
#Female 0
#Male 1즉, Female = 0, Male = 1 이라는 지시변수로 자동변환되어 모형에 포함되는 것이죠.
Male 요인이 1로 표현되기 때문에, 우리는 해당 지시변수를 포함한 회귀모형을 다음과 같이 표현할 수 있습니다.
Y = B0 + B1*I (gender = Male) + ε
-Male인 경우 : I = 1 ----> Y = (BO +B1) + ε
-Female인 경우 : I = 0 -----> Y = BO + + ε
library(cars)
head(Salaries, 5)
# rank discipline yrs.since.phd yrs.service sex salary
#1 Prof B 19 18 Male 139750
#2 Prof B 20 16 Male 173200
#3 AsstProf B 4 3 Male 79750
#4 Prof B 45 39 Male 115000
#5 Prof B 40 41 Male 141500
table(Salaries$sex)
#Female Male
# 39 358
class(Salaries$sex)
#[1] "factor"
선형 회귀모형에 데이터를 적합시켜봅시다.
Salaries 데이터는, 각 요소의 조건과, 급여를 나타낸 데이터 입니다.
우선, 성별(sex)와 급여(salary)간의 선형관계가 존재하는지 검토해봅시다.
model = lm(salary ~ sex, data = Salaries)
summary(model)
회귀 모형의 p-value 가 유의수준인 0.05 보다 충분히 작으므로 (0.005667), sexMale 지시변수는 급여에 상당한 영향을 부여함을 알 수 있습니다.
summary(model)$coef
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 101002.41 4809.386 21.001103 2.683482e-66
#sexMale 14088.01 5064.579 2.781674 5.667107e-03지시변수 sexMale (I(sex = Male)) 에 대한 회귀계수가 14088.01임을 알 수 있습니다.
따라서, 여성의 평균 급여는 10102, 남성의 평균 급여는 101002 + 14088 = 115090가 되겠습니다.
하나의 연속형 설명변수를 더 포함한 모형을 예시로 들자면,
Y = B0 + B1*X + B2*I + ε
-Male인 경우 : I = 1 ----> Y = (BO +B2) + B1*X + ε
-Female인 경우 : I = 0 -----> Y = BO + B1*X + ε
model_2 = lm(salary ~ sex+yrs.since.phd, data = Salaries)
summary(model_2)
박사학위를 딴 이후 햇수(yrs.since.phd) 변수가 포함된 이후, sexMale 지시변수의 p-value가 0.05 보다 큰것으로 나타났습니다. 반면에, yrs.since.phd 의 회귀계수에 대한 p-value는 0.05보다 상당히 작으므로, salariy에 상당한 영향을 미치는것으로 해석 됩니다.
summary(model_2)$coef
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 85181.8181 4748.3154 17.939377 4.925307e-53
#sexMale 7923.6239 4684.0813 1.691607 9.151167e-02
#yrs.since.phd 958.0793 108.3187 8.845004 3.109559e-17두 변수 모두 모형에 포함한다고 가정할때, salary = 85181 + 7023.6239*I(sex = Male) + 958*yrs.since.phd 로 회귀식이 표현가능하며,
-Male인 경우 : I = 1 ----> salary = 85181 + 7023.6239 + 958*yrs.since.phd
-Female인 경우 : I = 0 -----> salary = 85181 + 958*yrs.since.phd
<세개 이상의 범주(levels)를 포함한 범주형 변수>
세개 이상의 범주를 포함하는 변수를 포함한 회귀모형을 살펴봅시다.
세개 이상의 범주로 나누어야 하는 경우, 지시변수의 수를, 나누어야 하는 범주의 수 -1 로 채택하여 표현 할 수 있습니다.
지시 변수의 수 = 범주의 수 - 1
예를들어, 나누어야 하는 범주가 3개 인경우, 지시변수 두개 ( I(1), I(2) ) 가 필요하겠죠.
첫번째 범주는, I(1) = 1, I(2) = 0
두번째 범주는, I(1) = 0, I(2) = 1
세번째 범주는, I(1) = 0, I(2) = 0 로 표현 하게 됩니다.
나누어야 하는 범주가 4개인 경우, 지시변수가 세개 ( I(1), I(2), I(3) )가 필요하겠죠.
첫번째 범주는, I(1) = 1, I(2) = 0, I(3) = 0
두번째 범주는, I(1) = 0, I(2) = 1, I(3) = 0
세번째 범주는, I(1) = 0, I(2) = 0, I(3) = 1
네번째 범주는 I(1) = 0, I(2) = 0, I(3) = 0 으로 표현하게 됩니다.
하나의 설명변수와, 세개의 범주로 나누어지는 지시변수를 포함한 회귀모형은 다음과 같습니다.
Y = B0 + B1*X + B2*I(1) + B3*I(2) + ε
- 첫번째 범주에 속하는 존재하는 경우 : I(1) = 1, I(2) = 0 ---->Y = (B0 + B2) + B1*X + ε
- 두번째 범주에 속하는 경우 : I(1) = 0, I(2) = 1 ----> Y = (B0 + B3) + B1*X + ε
- 세번째 범주에 속하는 경우 : I(1) = 0, I(2) = 0 ----> Y = B0 + B1*X + ε
<R>
위에서와 동일한 Salaries 데이터에, 세개의 범주로 구분되는 rank 변수를 예시로 들어볼게요.
rank 변수는 세개의 범주를 포함하는 변수이기 때문에, 회귀모형에 수치형 변수로 포함되기 위해선, 두개의 지시변수가 필요하겠죠.
AssProf 범주는, I(1) = 0, I(2) = 0
AssocProf 범주는, I(1) = 1, I(2) = 0
Prof 범주는, I(1) = 0, I(2) = 1 로 표현 하게 됩니다.
table(Salaries$rank)
#AsstProf AssocProf Prof
# 67 64 266
contrasts(Salaries$rank)
# AssocProf Prof
#AsstProf 0 0
#AssocProf 1 0
#Prof 0 1
rank 변수만을 설명변수로 체택한, 회귀모형을 만들어봅시다.
model_3 = lm(salary ~ rank, data = Salaries)
summary(model_3)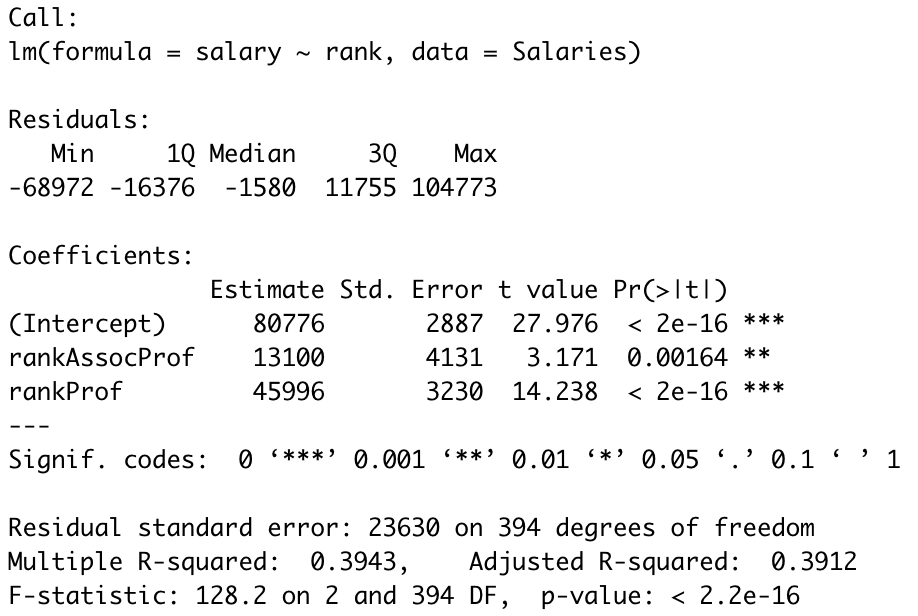
summary(model_3)$coef
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 80775.99 2887.313 27.976183 1.218762e-95
#rankAssocProf 13100.45 4130.850 3.171369 1.635999e-03
#rankProf 45996.12 3230.540 14.237906 2.101294e-37지시변수 rankAssocProf : I(rank = AssocProf) 에 대한 회귀계수가 13100.45 이고,
지시변수 rankProf : I(rank = Prof) 에 대한 회귀계수가 45996.12라는것을 알 수 있습니다.
salary = 80775.99 + 13100.45*I(rank = AssocProf) + 45996.12*I(rank = Prof)
두개의 지시변수의 회귀계수에 대한 p-value가 모두 0.05보다 작으므로, rank 변수가 salary에 상당한 영향을 미치는것으로 판단할 수 있습니다.
<변수 내 표준라인 레벨 (reference level) 바꾸기>
지시변수가 모두 0으로 표현되는 범주를 우리는 표준라인 레벨이라고 합니다.
즉, 기준이 되는 범주라고 해석해도 되겠죠.
sex 변수에서는 Female 범주가 기준(base; reference level)이 되고,
rank 변수에서는 AsstProf 범주가 기준(base; reference level)이 되는것을 확인하실 수 있으십니다.
contrasts(Salaries$sex)
# Male
#Female 0
#Male 1
contrasts(Salaries$rank)
# AssocProf Prof
#AsstProf 0 0
#AssocProf 1 0
#Prof 0 1이렇게 자동변환된 지시변수들을 회귀모형에 포함하게 되면, 우리는 기준이 되는 범주를 제외한 다른 범주들에 대한 지시변수를 모형에 포함하게 됩니다.
Female 범주에 대한 지시변수를 회귀모형에 포함하고 싶다면, reference line을 Male 로 바꿔주면 되겠죠.
똑같이, AsstProf 범주에 대한 지시변수를 회귀모형에 포함하고 싶다면, reference line을 AssocProf, 혹은 Prof 로 바꿔주면 됩니다.
Salaries$sex <- relevel(Salaries$sex, ref = "Male")
contrasts(Salaries$sex) #Male becomes base
# Female
#Male 0
#Female 1
Salaries$rank <- relevel(Salaries$rank, ref = "Prof")
contrasts(Salaries$rank)
# AsstProf AssocProf
#Prof 0 0
#AsstProf 1 0
#AssocProf 0 1바뀐 reference level을 가지고, 모형을 다시 만들어볼때, 우리는 Female 범주, AsstProf 범주에 대한 지시변수의 회귀계수를 검토할 수 있게 됩니다.
summary(lm(salary~sex, data = Salaries))$coef
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 115090.42 1587.378 72.503463 2.459122e-230
#sexFemale -14088.01 5064.579 -2.781674 5.667107e-03
summary(lm(salary~rank, data = Salaries))$coef
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 126772.11 1449.073 87.484947 3.243917e-260
#rankAsstProf -45996.12 3230.540 -14.237906 2.101294e-37
#rankAssocProf -32895.67 3290.466 -9.997269 4.024000e-21<교호작용>
교호작용(interaction)이란, 설명변수간의 상호작용에 의해 각각의 설명변수와 반응변수의 관계만으로는(산술적으로 단순히 두 변수가 미치는 영향의 합으로는), 두 설명 변수에 의해 일어나는 반응변수의 변화를 정확하게 예측 할 수 없는 경우를 말합니다.
예를들어, 고혈압은 유전적 요인과 비만 등 여러가지 요인에 의해 발생합니다.
비만과 유전적 요인에 의해, 고혈압이라는 질병의 유무를 예측한다고 하였을때, 비만과 유전적 요인에서 양의 교호작용이 일어나, 비만과 유전적 요인이 동시에 나타나는 경우, 고혈압의 위험성이 배 이상으로 더 늘어나는 경우 입니다.
비만인 경우 고혈압 발생 정도가 2배로 늘어난다고 하고, 부모 중 한명에게서 고혈압이 나타나는 경우, 자녀의 고혈압 발생정도가 4배로 늘어난다고 하였을때, 비만을 가지고 있고 동시에 부모에게서 고혈압이 관측된다면, 고혈압 발생정도가 8배가 된다고 예측할 수 있습니다.
하지만, 부모의 고혈압과 비만 사이에 양의 교호작용이 존재한다면, 두 요소가 모두 만족되었을때, 양의 교호작용에 의해 고혈압 발생정도가 8배를 넘게 됩니다.
Salaries 데이터의, 두개의 범주형 변수 rank, sex 사이에 양의 교호작용이 존재한다고 가정하고 회귀모형을 만들어봅시다.
<R>
1. 교호작용을 고려하지 않을때
salary = 127106 -4942 * I(sex = Female) -45519 * I(rank = rankAsstProf) -32457 * I(rank = rankAssocProf)
summary(lm(salary~sex+rank, data = Salaries))$coef
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 127106.594 1473.547 86.258956 1.779211e-257
#sexFemale -4942.951 4026.127 -1.227719 2.202874e-01
#rankAsstProf -45519.080 3251.761 -13.998287 2.082971e-36
#rankAssocProf -32457.821 3307.632 -9.813007 1.780462e-202. 교호작용을 고려할때
salary = 127106 - 5153* I(sex = Female) -45809 * I(rank= rankAsstProf) -32251 * I(rank = rankAssocProf) +1891 * I(sex = Female)*I(rank = AsstProf) +-1203*I(sex = Female)*I(rank = AssocProf)
summary(lm(salary~sex+rank+sex*rank, data = Salaries))$coef
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 127120.823 1503.456 84.5524189 2.292337e-253
#sexFemale -5153.211 5779.566 -0.8916260 3.731418e-01
#rankAsstProf -45809.358 3502.946 -13.0773809 1.137211e-32
#rankAssocProf -32251.119 3555.472 -9.0708406 5.825240e-18
#sexFemale:rankAsstProf 1891.656 9714.675 0.1947215 8.457121e-01
#sexFemale:rankAssocProf -1203.692 9992.086 -0.1204646 9.041770e-01위 예시에서는, 두개의 범주형 변수에 대한 교호작용을 고려한 경우를 보여드렸지만,
이 외에도, 연속형 변수-범주형 변수에도, 연속형변수 - 연속형변수 에도 교호작용이 존재할 수 있고, 이를 코드로 표현할수 있습니다!
<주의 >
지금까지 범주형 변수를 설명변수로 포함한 회귀모형과, R 코드에 대해 알아보았습니다.
범주형 변수에 대해 한가지 주의하실 점은,
반응변수가 범주형 변수인 경우, 오차의 정규성이 위배되기 때문에, 정규오차 선형회귀모형을 적용할 수 없다는점!
이 경우에는, 연속형 변수가 아닌 반응변수의 타입에 따라, 일반화 선형회귀(Generalized Linear Regression)을 적용하게 된다는점 잊지 말아주세요.
이 포스팅에서 다룬 핵심은! "설명변수"가 범주형 변수로서 모형에 포함되는 경우입니다.

