<통계적 추론 - Statistical Inference>
통계적 추론(Statistical Inference) 이란, 관측된 표본값들로 모수를 추정하고 모수에 대한 정보를 얻기 위한 방법입니다.
통계적 추론에는, 추정(estimation)과 가설검정(test of hypothesis)으로 구성됩니다.
오늘 포스팅에서는, 통계적 추론에서, 추정(estimation)단계를 다루겠습니다.
구체적인 추정(estimation) 방법으로는, 점추정(point estimation)과 구간 추정(interval estimation)이 있습니다.
점추정을 먼저 다뤄봅시다.
<점 추정 - Point Estimation>
점추정이란, 표본(sample)으로부터 구한 단일의 값(single value)으로 모수(parameter)를 추정하는 방법입니다.
예를들어, 우리가 관심있어하는 모수를 모평균(population mean)이라고 할때, 모평균을 추정하기 위해 쓰는 함수는 표본평균을 구하는 함수가 되고, 우리는 이를 추정량(estimator)이라고 부릅니다.

이 함수에, 직접 관측된 표본들(x1, x2, x3, ..., xn)을 대입해, 구한 추정값(estimate)이 점 추정값(point estimate)이 되는것이죠. 이렇듯, 점추정값은 모집단의 평균 혹은 모집단의 특성을 나타내는 모수들을 가장 '잘' 추정하기 위한 하나의 값으로 쓰입니다.

표본 평균 외에도, 모집단의 분산을 추정하기 위한 표본분산(Sample Variance)과 이의 제곱근인 표본표준편차(Sample Standard Deviation)역시 대표적인 점추정량 입니다. 모집단의 표본편차에 대한 추정량인 표본표준편차는 S를 사용하여 나타는것이 보편적입니다.

<점 추정 특징>
1. 비편향성 (Unbiasness)
좋은 추정량(estimator)은 모수(parameter)를 중심으로 하는 표본분포(Sampling distribution)를 가집니다. 따라서, 좋은 추정량은 비편향성(unbiasness)을 지니게 되죠. 추정량의 표본분포가 모수를 중심으로 분포한다면, 추정량의 평균은 모수의 값이 되고, 이 추정량을 우리는 비편향 추정량(unbiased estimator)이라고 합니다. 편향(bias)란 우리가 추정하고자 하는 모수와 추정량의 평균 차이로 계산됩니다. 따라서 추정량의 평균이 모수와 일치하는 경우, 그 추정량을 비편향 추정량으로 부르게 되죠.

모평균의 추정량으로 쓰이는, 표본평균은 비편향성을 지닙니다. 즉, 표본평균의 평균은 모평균이 되죠.

모분산의 추정량으로 쓰이는, 표본분산 역시 비편향성을 지닙니다. 즉, 표본분산의 평균은 모분산이 되죠.

<표본평균과 표본분산의 비편향성 증명>


2. 일치성 (Consistency)
표본의 크기가 무한대로 증가할수록, 추정량이 모수에 근접하려는 특성을 우리는 '일치성'이라고 합니다. 추정량이 모수에 확률추정(convergence in probability)하게 되는 성질을 우리는 추정량의 일치성(consistency)이라고 하며, 확률추정에 의한 일치성은 다음과 같이 나타내어 집니다.
0보다 큰 아주 작은, 가능한 모든 값인 ε에 대하여,
표본의 크기가(sample size ; n)이 무한대에 가까워질수록, 추정량인 Tn과 모수인 θ의 차이가 ε보다 클 확률은 0에 수렴한다는 정의입니다.

또한, 부등호의 방향을 바꿔 이렇게도 나타낼 수 있겠죠.

절댓값을 풀어, Tn에 대한 부등식으로 나타내면, 표본의 크기가 무한대에 수렴할수록, 추정량 Tn이 가지는 범위가 모수인 θ을 중심으로 하는 아주 작은(ε) 범위안에 존재한다는 정의이죠.

<표본평균일치성 증명>
1. Chebyshev's Inequality 이용
*전제) 위의 두 조건이 만족한다 ; 즉, 추정량의 평균이 모수이며, 표본크기가 커질수록 추정량의 분산은 0에 수렴한다.

2. Markov's Inequality 이용

3. 분산과 유효성 (Efficiency)
유효성이란, 두개 이상의 비편향 추정량이 존재할때, 어느 추정량의 분포가 더 모수에 집중적으로 분포하게 되는지를 나타내는 성질입니다.
즉, 추정량의 분산(Variance)과 표준편차(Sample deviation)와 관련된 개념이라고 할 수 있죠. 분산은 분포의 퍼짐정도를 나타내는 지표이기 때문에, 추정량의 유효성을 판단하기 위한 지표로서, 추정량의 분산이 쓰입니다.
*표본 추정량의 표준편차(sample standard deviation of the sample statistics)는 sampling error(표본 오차)라고 부릅니다.
비교하고자 하는 두가지 추정량이 모두 비편향 추정량(unbiased estimator)일때, 그 둘중 어떤 추정량을 모수를 추정하기 위해 채택해야 하는지를 결정할때 쓰이는 기준이 바로 유효성입니다. 이때, 두 추정량의 분산이 유효성을 판단하는 기준이 되는것이구요.
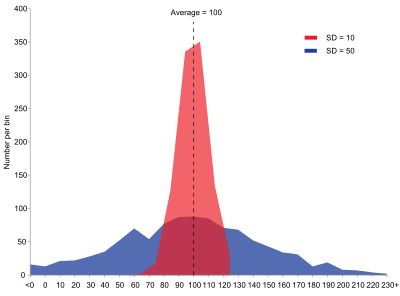
밑의 이미지에서 두 분포가 추정량이 가지는 확률분포라고 가정할때, 두 추정량이 모두 평균을 중심으로 분포하고 있는것을 볼 수 있습니다. 즉, 두 추정량 모두 비편향성을 지니는 것이죠. 하지만, 두 분포의 퍼짐정도는 다르게 나타나죠. 빨간색으로 분포가 표현된 부분은 표준편차(standard deviation)이 10이고, 파랑색 분포에는 표준편차가 50으로 나타난것을 불수 있습니다. 이 두 분포중에 어떤 분포가 더 유효성을 지닌다고 할 수 있을까요?
당연히, 평균을 중심으로 집중되어 분포된 빨간색 분포가 유효성(efficiency)을 지닌다고 할 수 있습니다.
따라서, 비편향 추정량들을 비교할때, 우리는 그들 중 가장 작은 분산을 가지는 추정량을 모수를 추정하기 위해 채택하겠죠. 비편향성을 가지며, 분산이 가장 작은 추정량을 '최소분산 비편향 추정량(Minimum Variance Unbiased Estimator)'이라고 합니다.
<점추정 방법의 종류>
점 추정에는 대표적으로 세가지 방법을 통해 이루어집니다.
각각의 추정법을 간략하게 설명 한후, 구체적인 내용은 별도의 포스팅으로 다루어 봅시다:)
- 모멘트 방법 (Method of Moments) : k차 표본 모멘트(k sample moments)를 모집단의 k차 모집단(k population moments)을 같다는 방정식을 풂으로써 모수를 추정하는 방법
- 최대 가능도 추정법 (Maximum Likelihood Estimation ; MLE) : 관측된 표본을 대한 가능도(likelihood)를 가장 크게 만드는 모수를 추정하는 방법
- 베이즈 추정법 (Bayes Estimation) : 모수를 확률변수로 여기며, 관측된 표본을 고려하여 업데이트된 사전분포(prior distribution)인 사후분포(posterior distribution)를 이용하여, 손실함수(loss function)을 최소화하는 추정값을 찾음으로써, 모수를 추정하는 방법.
<점추정의 한계>
점추정(Point estimate)은 표본으로부터 구한 단일의 값이기 때문에, 점추정값은 그 추정값이 얼마나 모수에 가까운지에 대한 정보를 포함하지 않습니다.
점추정은 관측된 표본들로만부터 추론된 하나의 값으로만 구해지기 때문에, 표본의 크기가 작은경우 모집단의 특성을 잘 반영하지 못하는 경우가 생길 수 있습니다. 이 점추정의 한계를 극복하기 위해 고안된 방법이, 구간 추정(Interval Estimate)는 모수가 있을 것으로 예상되는 값의 범위를 제공합니다. 따라서, 점추정값의 정확도를 제공해주죠.
다음 포스팅에는, 구간추정에 대한 내용을 다뤄보도록 합시다:)
'Statistics' 카테고리의 다른 글
| 표본추출법 / 확률적 표본추출/ 단순임의추출, 체계적추출, 층화임의추출, 군집추출 (0) | 2021.05.25 |
|---|---|
| 중심 극한 정리(CLT)와 R / Central Limit Theorem and R (0) | 2021.05.18 |
| 모분포와 표본분포, 표본추출의 규칙 / Population distribution and Sampling distribution (0) | 2021.05.17 |
| 정규분포 / 68-95-99.7 규칙/ 표준정규분포 / R (1) | 2021.05.13 |
| [회귀]다중공선성 / Multicollinearity / R (0) | 2021.02.17 |