회귀분석에서는, 오차에 대한 가정을 전제로 최소제곱법에 의한 추정이 가능합니다.
1. E( εi ) = 0
2. Var( εi ) = σ^2 * Ι "등분산성"
3. Cov( εi, εj) = 0 "독립성"
회귀식을 추정할때, 가장 근본이 되는 원리인 '최소제곱법'에 의한 회귀식은 , 오차의 등분산성과 독립성에 의해 '최량 선형 비편향 추정량'이 되죠. 최량선형 비편향 추정량이란, '추정량이 그 어떠한 모수에 대한 추정량보다 분산이 작다. 즉, 최고의 추정량이다' 라는 뜻입니다.
오차에 대한 등분산성과 독립성에 의해 '최소제곱법에 의한 추정량은 최량선형 비편향 추정량이다' 라는 가우스 마코브 정리가 성립되는것이죠.
이를 조합해보면, 오차의 분포에 대한 가정은 기본적으로 εi~N(0, σ^2)인것이죠. 정규성에 대한 가정은 회귀분석에서 최소제곱법으로 구한 추정량의 분포에서 모수들에 대한 추론을 위해서 필요합니다.
보통은 표본을 가지고 회귀식을 추정하기 때문에, 모집단으로부터 추정한 회귀식으로부터 얻은 예측값과 실제값의 차이인, 오차는 관측할수 없는 값입니다. 따라서, 우리는 오차에 대해 '모든 오차는 동일한 분산을 가진다', '오차간에 서로 영향을 주지 않는다' 라는 가정을 전제하고, 회귀식을 추정하는 것이죠. 하지만, 오차에 대한 정보가 구체적으로 명시되어 있고, 그것이 오차에 대한 가정에 어긋나는 경우, 이를 무시하는것은 옳지 않습니다. 위의 가정들을 옳다고 가정하고 모형을 추정하지만, 확실하게 오차가 위의 가정을 위반하는것이 관측되면, 이에 대한 교정과정을 거치는것이 통상적 절차입니다. 또한, 오차가 관측되지 않은 변수임에도 불구하고, 오차의 정규성에 대한 검토가 가능한데, 이에 대한 진단은 잔차에 기초합니다. 잔차가 오차의 선형결합으로 표현되기 때문이죠.
잔차는 관측값과, 표본으로부터 추정한 회귀식에 의한 적합값의 차이를 나타냅니다. 잔차에 대한 자세한 설명은 https://jangpiano-science.tistory.com/116?category=875432 를 참고해 주세요.
오차와 잔차
<오차와 잔차> 오차와 잔차는 표기방식부터, 해석, 조건까지 정확하게 다른 값입니다. 오차(error)는 모집단(population)으로부터 추정한 회귀식으로부터 얻은 예측값과 실제 관측값의 차이를 이야기
jangpiano-science.tistory.com
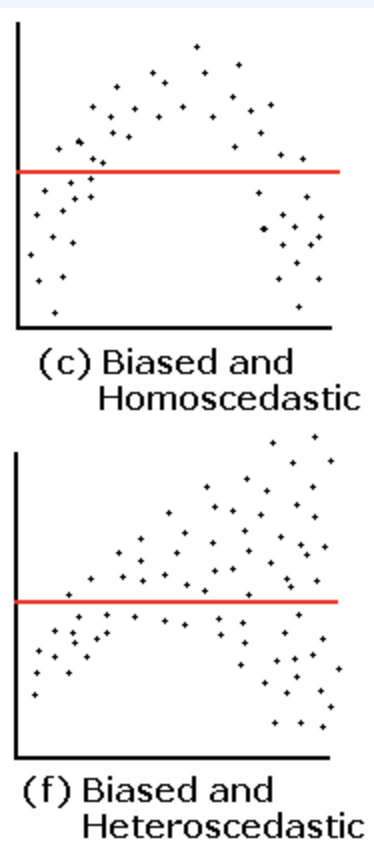
회귀식을 추정하기 위한 중요한 가정의 타당성을 의심하여, 모형에 어떠한 문제점이 존재하는지 알아보는 진단을 '모형진단(model diagnostics)'라고 합니다. 이번 포스팅에서는, 잔차의 분포를 바탕으로 오차에 대한 가정의 타당성과 추정한 선형회귀모형의 타당성을 의심해보도록 하겠습니다. 잔차의 분포를 한눈에 살펴볼 수 있는 산점도(scatter plot)들을 통해, 잔차의 분포를 살펴봅시다.
<잔차산점도 residual plot>
x축 : 회귀식에 의한 적합값
y축: 잔차(ei) or 스튜던트화 잔차(ri)
*스튜던트화 잔차(ri)는 '표준화된 잔차'로 모형 진단에서 주로 표준화되지 않은 잔차(ei)를 대신하여 사용합니다.
<잔차산점도 R 코드>
plot(x = fitted(lm(Y~.,data = )), y = rstandard(lm(Y~., data = )))
- 적합 모형
: 잔차산점도가 -3과 3 사이에 고르게 분포되어 있음. (잔차산점도의 회귀선 기울기 = 0)
회귀식이 설명변수와 반응변수사이의 선형의 관계성(linearlity)을 나타내기에 적합하고, 오차에 대한 가정이 만족된다면, 잔차산점도가 y축을 기준으로 -3과 3 사이에 고르게 분포되고, 특별한 규칙성을 나타내지 않습니다.
-부적합 모형
1. 오차의 이분산성(Heteroscedasticity) : 적합값(x축)이 증가함에 따라, 스튜던트화 잔차(y축) 값의 퍼짐 정도가 증가하거나, 감소.
이미지 (d)를 보자면, x축 값(적합값)이 증가함에 따라, y축 값(ri)의 퍼짐 정도가 같이 증가하는것을 볼 수 있죠.
이미지 (e)역시, (d)만큼 뚜렷한 퍼짐정도를 보이진 않지만, x축 값이 증가함에 따라, y축 값의 퍼짐 정도가 같이 증가하는것을 볼 수 있습니다.
이미지 (f)에서는, x축 값이 증가함에 따라 y축 값의 퍼짐 정도가 일정하다가 증가하죠.
이 이미지들은 모두 오차의 이분산성을 나타낸다고 볼 수 있습니다. 따라서, 다음과 같은 잔차산점도가 관측된다면, 우리는 모형에 대한 적절한 변형이 필요하겠죠. 오차의 이분산성이 발견되었음에도 불구하고, 이를 무시하고 최소제곱법에 의한 회귀모형을 받아들이는것은 바람직하지 않습니다.
이분산의 증거가 분명히 발견된다면, 반응변수에 변환을 취한다던지, 가중최소 제곱법을 사용해야 합니다.
2. 회귀모형의 비선형성(non - linearlity) : 적합값(x축)에 대하여, 스튜던트화 잔차(y축) 값이 곡선의 형태를 보여줌.
이미지 (d)를 보자면, x축 값(적합값)이 증가함에 따라, y축값(ri)가 곡선의 형태를 띄는것을 보실 수 있으시죠.
이미지 (f)에서 역시, x축 값(적합값)이 증가함에 따라, y축값(ri)가 곡선의 형태를 띕니다.
우리는 최소제곱법에 의해 잔차의 제곱합을 최소로 하는 하나의 선을 회귀식으로 추정합니다. 따라서 선형 추정량이라고 하죠.
하지만, 다음과 같은 잔차산점도가 발견된다면, 회귀식에 이차항을 포함시키라는 뜻으로 해석됩니다. 즉, 선형 모형이 바람직하지 않다는것으로 해석이 가능하죠. 따라서, 다음과 같은 잔차산점도를 발견한다면, 변수변환을 통해 회귀식을 구성하는 항을 변환시켜주어야 바람직합니다.
<잔차 - 설명변수 산점도 residual versus predictor plots>
잔차산점도(residual plot)을 이용해, 회귀모형의 비선형성(non - linearlity)을 관측하였다면, 어떠한 설명변수에 의한 비선형성인지 알아내야 변수에 적절한 변형을 취할 수 있겠죠? 즉, 어떠한 설명변수에 적절한 변형을 취해야 하는지 알기 위해서는, 어떤 설명변수가 잔차와의 비선형성을 갖는지 알아야 합니다. 잔차-설명변수 산점도를 통해서 이에대한 정보를 얻을 수 있습니다.
x축: 검토하고자 하는 설명변수 ----> X1 or X2
y축: 전체 설명변수에 대한 회귀적합 후 잔차 ----> e(Y|X1, X2)
잔차-설명변수 산점도 역시, 모형이 잘 적합되었다면 특별한 형태를 띄지 않을것입니다. 하지만, X1을 x축으로 하고 e(Y|X1, X2)를 y축으로 한 산점도에서, 비선형 모형이 나타나는 경우, X1변수에 변환이 필요합니다.
<잔차-설명변수 산점도 R 코드>
plot(x = X1, y= resid(lm(Y~., data = ))) #X1의 잔차-설명변수 산점도
plot(x = X2, y= resid(lm(Y~., data = ))) #X2의 잔차-설명변수 산점도
예를들어, x축을 X1로 하고, y축을 전체 설명변수에 대한 회귀적합 후 잔차로 설정하였을때, 다음과 같은 산점도가 나타난다면, 이는 X1이 증가함에 따라 잔차가 비선형의 모양을 하는것이 보이므로, X1의 이차항을 모형에 포함시켜야 함을 알 수 있습니다.

<정규 확률 그림 Normal probability plot>
회귀분석에서의 중요한 또한가지의 가정은, 오차의 정규성입니다. 오차가 평균을 0으로, 분산을 σ^2로 가지는 정규분포를 따른다는 가정은 회귀분석에서 모수에 대한 검정과 신뢰구간을 구하는데 필요합니다. 카이제곱분포, t 분포와 정규분포와의 관계성 덕분에, 회귀분석에서 F 검정과 t검정이 유의한것이죠. 오차의 정규성에 대한 검정 역시, 오차는 관측할 수 없는 값이기 때문에, 잔차에 의존합니다. 설명변수의 수가 고정되어있고, 표본의 크기가 증가하면, 잔차의 정규성 검토로, 오차의 정규성을 검정할 수 있습니다.
정규 확률 그림을 그리는 방법은 다음과 같습니다.
1. 관측값(표본)을 작은것에서 큰순으로 나열한다. (표본의 순서통계량)
2. 각 자료에 해당하는 정규점수(normal score)를 계산한다.
3. 정규점수를 x축으로, 관측값(표본)의 순서통계량을 y 축으로 한 산점도인 '정규 확률 그림'을 그린다.
정규점수(normal score)란, 자료가 평균으로부터, 표준편차의 몇배만큼 떨어져있는지 보여주는 값입니다. 표준정규분포 (N(0,1))에서 관측값이 평균으로부터 얼마나 떨어져있는지를 기록한 경계값이라고 할 수 있죠. 정규분포는 평균에 밀집된 종 모양을 띄고 있으므로, 우리가 관측한 값이 정규분포에서 추출된 값인지 검토하기 위해서는, 정규분포와 비슷한 분포도를 가져야 겠죠. 만약, 관측값들이 평균에 밀집된 종 모양을 띄고 있으면, 정규분포에서 추출되었을 확률이 높아지는 것입니다. 관측값의 개수가 10개라고 하였을때, 정규분포를 10개의 등확률 구간으로 나눈후 경계값과 비교하였을때, 큰 차이가 없다면, 관측값은 정규분포로부터 추출되었다고 결론 내릴 수 있습니다. 정규 확률 그림이란, 정규점수를 x축으로, 관측값(표본)의 순서통계량을 y 축으로 한 산점도입니다. 따라서, 관측값이 정규분포로부터 추출된 값이라고 하였을때, 정규 확률 그림은 일직선에 접근하게 됩니다.
우리는 오차의 정규성에 대하여 관심이 있기 때문에, 잔차의 정규성을 검토하게 되는것이죠. 따라서, 구체적으로 오차의 정규성을 검정하기 위한 정규확률 그림을 그리는 방법은 다음과 같습니다.
1. 관측된 잔차를 작은것에서 큰순으로 나열한다. (잔차의 순서통계량)
2. 각 잔차에 해당하는 정규점수(normal score)를 계산한다.
3. 정규점수를 x축으로, 잔차의 순서통계량을 y 축으로 한 산점도인 '정규 확률 그림'을 그린다.
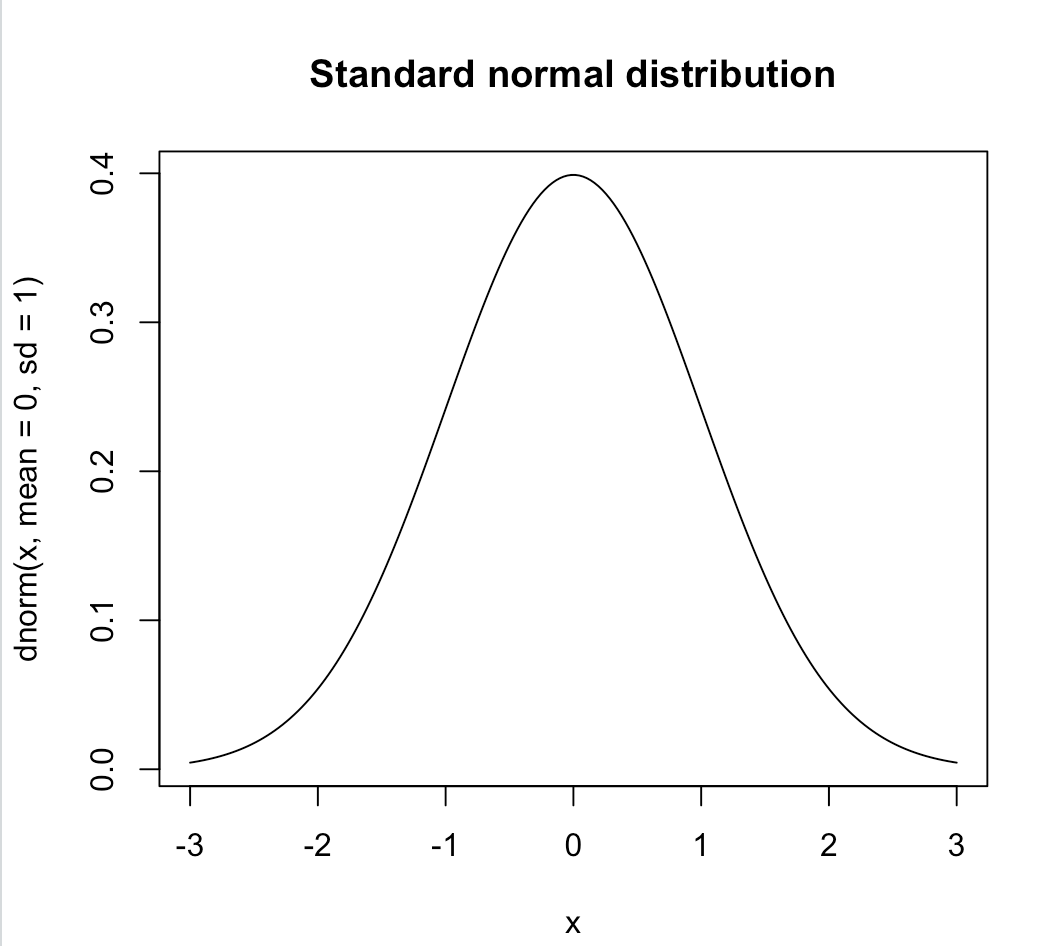
*R 코드로 만들어본 정규분포 그래프
> x <- seq(-3, 3, length = 200)
> plot(x, dnorm(x, mean=0, sd=1), type='l', main="Standard normal distribution")
<정규확률그림 R 코드>
-정규확률 그림 그리는 방법에 의한, 정규확률 그림 그리는 법 요약 코드
qqnorm_function = function(Z){
Z <-sort(Z) #관측값(표본)의 순서통계량(order statistics)
Q = qnorm(((1:length(Z))-0.3175)/(length(Z) + 0.365)) #정규점수(normal score)
plot(x = Q, y = Z, xlab = "normal data", ylab = "ordered observed data")
}
#Q = qnorm((1:length(Z))/length(Z))로 설정하면, 정규분포는 (-inf, +inf)의 분포이므로, inf 값을 프린트한다. 따라서, 이를 방지하기 위해 일반적으로 0.3175, 0.365를 빼고 더해주어, inf값을 프린트 하지 않게 해준다.
-정규확률 그림 그려주는 R 내장 함수
qqnorm(resid(lm(Y~X)))
평균을 10으로, 분산을 1로 하는 정규분포에서 100개의 표본을 추출하였다고 하였을때, 이 표본값들을 정규점수와 비교하는 정규 분포 그래프를 그려보겠습니다. 당연한 결과로, 정규 분포 그래프가 일직선을 나타내는것을 보실 수 있습니다.
> X<-rnorm(100, 10, 1)
> qqnorm(X)

그렇다면, 반대로, 정규분포가 아닌, 최솟값을 -10, 최댓값을 10으로 하는 균등분포(Uniform distribution)에서 100개의 표본을 추출한 후, 정규분포 그래프를 그리면, 일직선이 아닌 형태의 그래프가 그려지는것을 보실 수 있습니다.
> X<-runif(100, -10, 10)
> qqnorm(X)

<Shapiro-Wilk Normality Test>
위에서 언급한 QQ-plot을 이용한 시각적 해석 이외에도, shapiro.test를 통해 데이터가 오차의 정규성을 만족하는지 확인 할 수 있습니다. R에서 샘플을 바탕으로, 전체데이터의 정규성을 시험하기 위해 사용되는 shapiro test 의 R 코드는 다음과 같습니다. 우리의 목적은 '오차'의 정규성이니, shapiro.test 함수 안에 resid(lm(Y~X)를 넣어주면 되겠죠?
shapiro.test(resid(lm(Y~X)))
shapiro 분석에서,
귀무가설(H0; Null hypothesis) : 데이터의 분포가 정규분포를 따른다 (정규성 만족)
대립가설(Ha; Alternative hypothesis) : 데이터의 분포가 정규분포를 따르지 않는다 (정규성 위배)
입니다.
따라서, shapiro test의 결과값에서 p-value가 유의수준(significance level)보다 작으면, 귀무가설을 기각하므로, 정규성이 위배된다는 결론을 내리게 되며, p-value가 유의수준보다 크게 되면, 귀무가설을 기각하는것을 실패하므로, 정규성의 가정이 위배되기에 근거가 충분하지 않다는 결론을 내리게 됩니다.
<W-통계량>
위에서, 정규 확률 그림(normal probability plot)을 통해 오차의 정규성을 검토하는 방법을 소개하였습니다. 이 방법 이외에도 정규성을 검정하기 위한 방안이 많이 제안되었지만, 그중에서도 Shapiro와 Wilk에 의해 고안된 Shapiro-Wilk 통계량, 간단히 말해 W-통계량을 설명하겠습니다.
W-통계량은 정규 확률 그림에서 X축, Y축을 형성하던, 정규점수와 관측값의 순서통계량의 상관계수(Correlation coefficient)의 제곱값입니다.
-W-통계량을 이용해, 오차의 정규성을 검토하는 R 코드
>?shapiro.test

>shapiro.test(resid(lm(Y~X)))
다음의 코드로부터 나온 p-value가 0.1보다 작다면, 오차의 정규성이 기각됩니다.
<스코어 검정 score test>
스코어 검정은, 오차의 등분산 가정에 대한 검정법입니다. 오차의 등분산 가정이란, 모든 관측값에 대해 오차의 분산이 같다는 뜻입니다. 이는, 모든 X의 값에 대해 Y의 분산은 같다는 가정이 되기도 하죠. 그러나 설명변수와 반응변수 혹은 외적요인에 의해 오차의 분산이 이루어지지 않는 경우도 있습니다.
위에서 잔차산점도와 설명변수-잔차산점도에서 X축이 증가함에 의해 Y축의 퍼짐 정도가 달라짐을 파악하며 등분산에 대한 대략적인 진단에 대해 소개하였습니다. 하지만, 산점도를 통해 오차의 이분산성을 파악하는것이 애매한 경우, 우리는 주관적인 판단에 의존해야만 합니다. 따라서, 산점도만을 통해 이분산성을 파악하는데에는 한계가 존재하므로, 스코어 검정(score-test)라는 이분산성을 판단하는 통계적인 방법이 제시되었습니다.
스코어 검정을 시행하는 단계는 다음과 같습니다.
H0: 등분산 (homoscedestic)
H1: 이분산 (heteroscedestic)
1. 추정회귀식과, 그에 따른 잔차 ei 를 구한다.
2. 조정된 제곱잔차 ui 를 구한다.
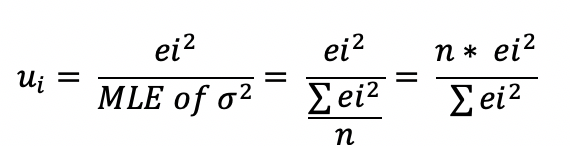
3. 반응변수를 U로, 설명변수를 Z로 회귀식을 추정한다. (Z : 오차의 값에 영향을 준다고 생각되는 변수 --> 만약 설명변수 X1이 오차와 상관관계가 있다고 생각되는 경우, Z를 X1로 취하고, 반응변수 Y가 오차와 상관관계까 있다고 생각되는 경우, Z를 Y로 취한다.)
4. 3번에서 구한 회귀식에서 회귀제곱합(SSreg)을 구한다.
5. 회귀제곱합의 절반을 구함으로써 스코어 검정 통계량을 구한다. 즉, 스코어 검정 통계량은 SSreg/2
(자유도: Z에 포함되는 설명변수의 수 : q)
6. 스코어 검정 통계량과 자유도를 q로 하는 카이제곱 분포를 비교하여 등분산 가정을 기각할지 말지 정한다.
스코어 검정 R 내장 함수
> ?car::ncvTest

> car::ncvTest(lm(Y~X))
스코어 검정 시행 단계에 따라 R 코드를 짜보았습니다.
Z는 반응변수를 U로 하여 회귀시키고자 하는 설명변수입니다. 제가 작성한 코드는, 하나의 설명변수로 가정하고 작성한 코드임으로, 두개 이상의 설명변수에 대한 스코어 검정을 위해서는, 코드의 변경이 필요합니다.
a는 유의수준(significant level)으로, 오차가 등분산이라는 귀무가설을 기각할지 말지 결정하는것에 기준이 되는 값입니다.
#a : significance level
#Z : variable that is supposed to affect variance
score_test = function(X, Y, Z, a){
print("have a quick look at residual scatter plot for checking the Heteroscedasticity")
plot(x = fitted(lm(Y~X)), y = rstandard (lm(Y~X)))
#process to have adjusted squared error
mle_var = sum(resid(lm(Y~X))^2)/length(X)
U = resid(lm(Y~X))^2/mle_var
print("H0 :[Equal Variance] Variance does not rely on Z")
print("H1: [Heteroscedasticity] Variance relies on Z")
test = lm(U~Z)
score_test_statistics = anova(test)[1,2]/2
df = anova(test)[1,1]
p_value = 1-pchisq(score_test_statistics, df)
print(paste("p-value is", p_value, collapse = " "))
if (p_value<a){
print("reject null hypothesis because p-value is small enough--> Heteroscedasticity ")
}
else {
print("do not reject null hyoothesis because p-value is not that small--> Equal Variance")
}
}
<더빈 - 왓슨 통계량 >
더빈 - 왓슨 통계량(Durbin - Watson statistics)이란, 오차항의 독립성을 검정하는데 기준이 되는 통계량입니다.
오차의 독립성 가정이란, 모든 관측값에 대해 오차간의 상관관계가 없다는 뜻입니다. DW 통계량이라고 불리우는 더빈 - 왓슨 통계량을 이용하면, 잔차들의 상관계수를 측정하여, 오차의 독립성을 검정할 수 있습니다.
오차의 독립성은 선형회귀분석의 성립되어야 하는 가정으로써, 더빈 왓슨 통계량을 통한 오차항 독립성 검정에서 귀무가설과 대립가설은 다음과 같습니다.
H0(귀무가설 : Null hypothesis) : 각 오차들은 서로 독립이다.
H1(대립가설 : Alternative hypothesis) : 어떠한 오차는 서로 상관관계를 가진다.
DW 통계량은 다음과 같이 구하고,

DW 통계량이 2.0 에 인접하면, 오차항간의 상관관계가 없는것을 의미하며,
DW 통계량이 0~2.0 인 경우 , 오차항간의 양의 상관관계,
DW 통계량이 2.0 ~ 4.0 에 인접하면, 오차항간의 음의 상관관계가 있는것으로 검정합니다.
더빈 - 왓슨 통계량 R 내장 함수
lmtest::dwtest(lm(Y~X))
회귀모형의 오차 가정에 대한 전반적인 검정 R 코드
>?gvlma

>install.packages("gvlma")
>gvlma::gvlma(lm(Y~X))
해석


해석:
Global Stat: 전반적인 가정에 대한 결과
Skewness: 정규성
Kurtosis: 정규성
Link Function: 선형성
Heteroscedasticity: 등분산성
이상, 지금까지 몇가지 산점도와 통계량을 바탕으로 회귀모형에서 오차에 대한 가정(등분산성)과 회귀모형의 선형성에 대한 검토를 수행해 보았습니다.
감사합니다:)
'Statistics' 카테고리의 다른 글
| [회귀]지수변수를 설명변수로서 포함한 회귀 모형, 교호작용에 대한 설명/ Indicator variable in regression model, Interaction / (0) | 2021.02.15 |
|---|---|
| [회귀]회귀모형에서 이상점과 영향력 있는 관측값 검정 (1) | 2021.02.11 |
| [회귀] 다중회귀에서의 분산분석과 수정결정계수/ Anova in Multiple Regression / (1) | 2021.02.01 |
| [회귀]오차와 잔차, 표준화 잔차 (2) | 2021.01.29 |
| [회귀] 행렬을 이용한 다중회귀 모형, 최소제곱법에 의한 추정 (5) | 2021.01.21 |